はじめに
安冨歩さんという方がいらっしゃいます。 私は大学生になって間もない頃、図書館で「経済学の船出」を読み、こんな経済学者がいるのかと衝撃を受けたのですが、今日はそんな経済学者が作った貨幣の生成や崩壊のMAS(マルチエージェントシミュレーション)モデルを紹介します。
モデル自体は1995年に論文「The emergence and collapse of money」で発表され、2000年には書籍として「貨幣の複雑性: 生成と崩壊の理論」(以降、書籍)が出版されています(書籍は出版社が潰れたため現在は中古市場で高値取引されています)。 モデルは拡張性が高く、暗号通貨や基軸通貨の分析などの研究でベースとして現在も利用されています(応用例は別記事で紹介します)。
モデルは3種類ありますが、いずれも人工的な市場(しじょう)というよりも人工的な市場(いちば)に近いモデルです。 3つのモデルから、段階的に貨幣の生成や崩壊の設定を探っています。 最終的なモデル(進化的モデル)ではエージェントのシンプルな行動ルール(欲求、需要、生産、消費、情報交換、戦略の変更)から貨幣の生成や崩壊という複雑な現象を再現しています。
ここでは基本的に書籍を参照して、モデルのみを紹介します(背景の思想等については別の記事で紹介します)。 詳細を知りたい方は書籍をあたってください。
モデルの種類
書籍では、
- 物々交換のモデル(欲望の二重一致の困難さを確認)
- 貨幣的交換のモデル(貨幣の生成メカニズムを確認)
- 進化的モデル(貨幣の生成と崩壊メカニズムを確認)
という順序で発展的にモデルを作成しています。 以下、それぞれについて紹介します。
共通する設定
その前にモデルで共通する設定を紹介します。
- 1ターンで全てのエージェントはそれぞれ1回ずつ需要→交換→消費・生産のサイクルを実行する
- あるエージェントが生産する商品は1種類で、シミュレーションの途中でエージェントが生産する商品は変化しない
- エージェントは、最初に自分が生産した商品を1つ所有している
- 各エージェントは最初に自分が欲求する商品を決める
- エージェントは、自分が生産した商品は欲求しない
エージェントは以下のパラメータを持ちます。 $$Agent_i = (w_i, p_i, \boldsymbol{h_i}, \boldsymbol{d_i}, u_i)$$
- $w$ - 欲求する商品:エージェントが消費したい対象で、所有する場合は消費ステップで全て消費する
- $p$ - 生産する商品:エージェントが生産する商品
- $\boldsymbol{h}$ - 所有ベクトル:エージェントが持っている商品のベクトル
- $\boldsymbol{d}$ - 需要ベクトル:エージェントが消費したいと考えているかに関わらず需要している商品のベクトル
- $u$ - 効用水準:所有している$w$を消費して増加する、エージェントの得点
ここで、欲求と需要を区別していることに注意します。
また、シミュレーションには以下のパラメータがあります。
- $N$ - エージェント数
- $C$ - 所有費(書籍では運送費ですが、モデルは距離的なロジックを持たないため所有としています)
- $P$ - 生産費
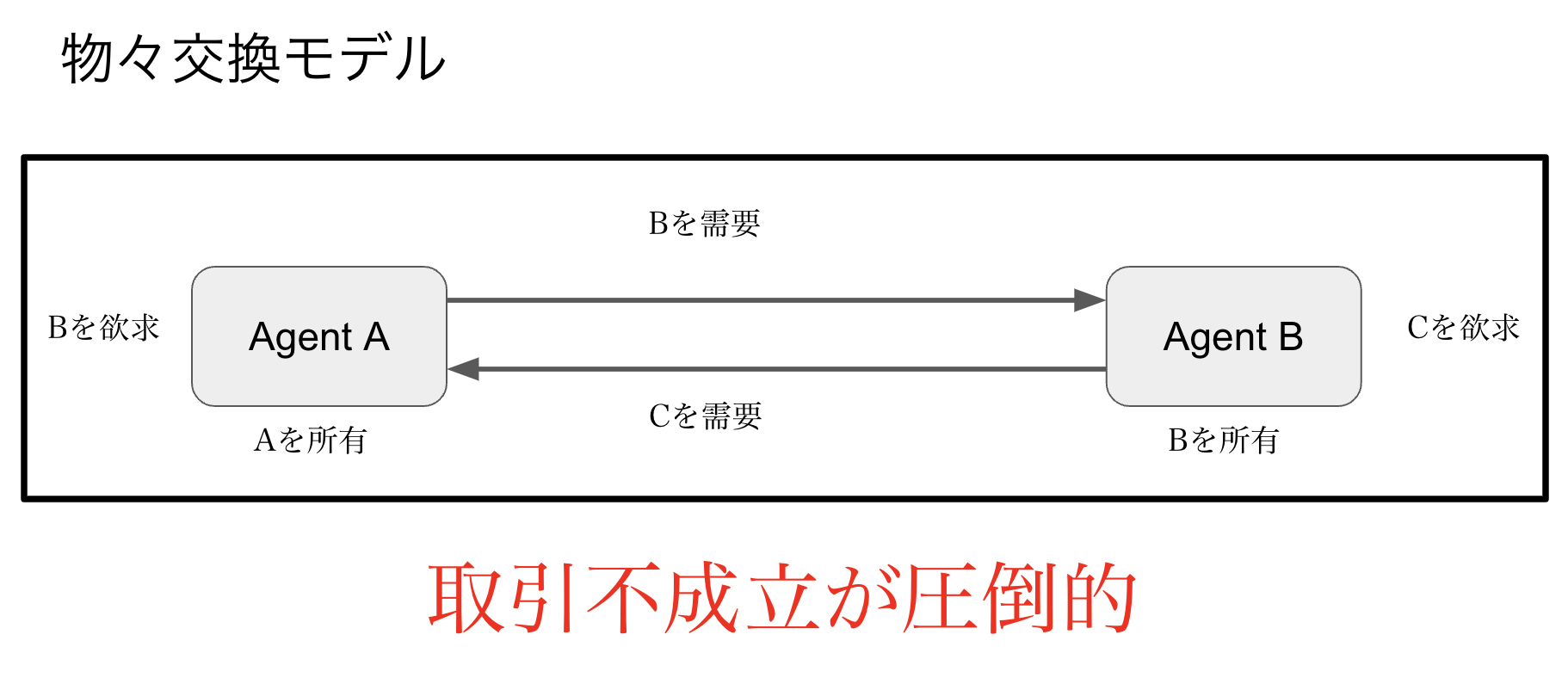
物々交換モデル
パラメータ
書籍では、以下のパラメータが使用されています。
- $N = 50$
- $C = 0.001$
- $P = 0.02$
エージェントの行動ステップ
1ターンの初めに全てのエージェントをランダムに配列します。 その後、配列の最初からそれぞれStep1~4を実行します。 全てのエージェントで実行し終えると配列し直して、次のターンが始まります。
以下のステップは抽象化されすぎていると思われるかもしれませんが、これはステップの一部が次節以降のモデルでも利用されるためです。
Step1: エージェントの選出
配列からエージェント1体(Aとします)を取得し、そのエージェントが欲求する商品を最も多く持っているエージェントを指定します(Bとします)。
Step2: 需要ベクトルの算出
Aは自分が欲求する商品について、Bが持っている全てを需要します。 Bは自分が欲求する商品について、Aが持っている全てを需要します。 エージェントAの欲求する商品$w_a$($w_a = Agent_{A}.w$)(ここで$Agent_{A}.w$の$w$はエージェントAの$w$を表します)について $Agent_A.d_{w_a} = Agent_B.h_{w_a}$ であり、Bも同様です。
Step3: 商品の交換
商品の交換が成立するためには
- 自分が需要する商品の全てを相手が所有していること
- 相手が需要する商品の全てを自分が全て所有していること
- 1対1の数量で交換すること、つまり交換する商品の総量(交換総量)を等しくすること
が必要です。 そこでエージェントの受容する商品の総量(需要総量)をそれぞれ算出し、需要総量で場合分けして交換総量を揃えます。 エージェントAの需要総量は$D_A = \sum_{j=1}^{N}Agent_A.d_j$で算出します。
[1] $D_A = D_B = 0$の場合
交換は行われないため、次のステップに移ります。
[2] $D_A = D_B \gt 0$の場合
AとBは需要している商品を1対1で交換します。 この場合、全ての需要ベクトルは所有ベクトルに変わるため、AとBが需要した全ての商品$j$について、 $$Agent_A.h_j \mathrel{+}= Agent_A.d_j - Agent_B.d_j$$ $$Agent_B.h_j \mathrel{+}= Agent_B.d_j - Agent_A.d_j$$ という操作を行った後で、 $$Agent_A.d_j = 0$$ $$Agent_B.d_j = 0$$ とします。
引き算しているのは、自分が需要している商品を相手も需要している可能性があるためです。
[3] $D_A \gt D_B$の場合($D_B \gt D_A$の場合は以下AとBを逆にする)
Aは$D_A$のうち、$D_B$単位だけBに交換を要求できます。 以下のルールに従って、できるだけ多様な商品を交換します。
以下の操作を$D_B$回行います。
- $Agent_B.h$のうち、最小の$Agent_B.h_j$である$j$を選ぶ(複数ある場合、その中からランダムに選ぶ)
- $Agent_A.h_j \mathrel{+}= 1$
- $Agent_B.h_j \mathrel{-}= 1$
- $Agent_A.d_j \mathrel{+}= 1$
Step4: 消費と生産
全てのエージェントで以下のように$Agent_i.u$を算出します(ここではエージェントAを例に記述します)。
- 所有する商品のコストを引く
- 欲求する商品を所有する場合、全て消費し、消費数だけ足す
- 自分の商品を所有していない場合、所有を1増やし生産コストを引く
具体的には、以下のような操作を実行します。
消費は $$Agent_i.u \mathrel{-}= C \times \sum_{j=1}^{N}Agent_A.h_j$$ $$Agent_i.u \mathrel{+}= Agent_A.h_{Agent_A.w}$$ です。 また、$Agent_A.h_{Agent_A.w} \gt 0$の場合は確実に、$Agent_A.h_{Agent_A.w} = 0$の場合は低確率で$Agent_i.w$をランダムに変更します。 低確率で変更するのは、モデル内で交換可能な組み合わせがなくなった状態に陥ってしまうのを避けるための攪拌です。 その後、$Agent_A.h_{Agent_A.w} = 0$とします。
生産は、$Agent_A.h_{Agent_A.p} = 0$ならば、 $$Agent_A.h_{Agent_A.p} = 1$$ $$Agent_A.u \mathrel{-}= P$$です。
結果
物々交換モデルでは、エージェント同士の交換がほとんど起こらないことが確認されます。 これは欲望の二重一致の困難さを示していると考えられます。
貨幣的交換モデル
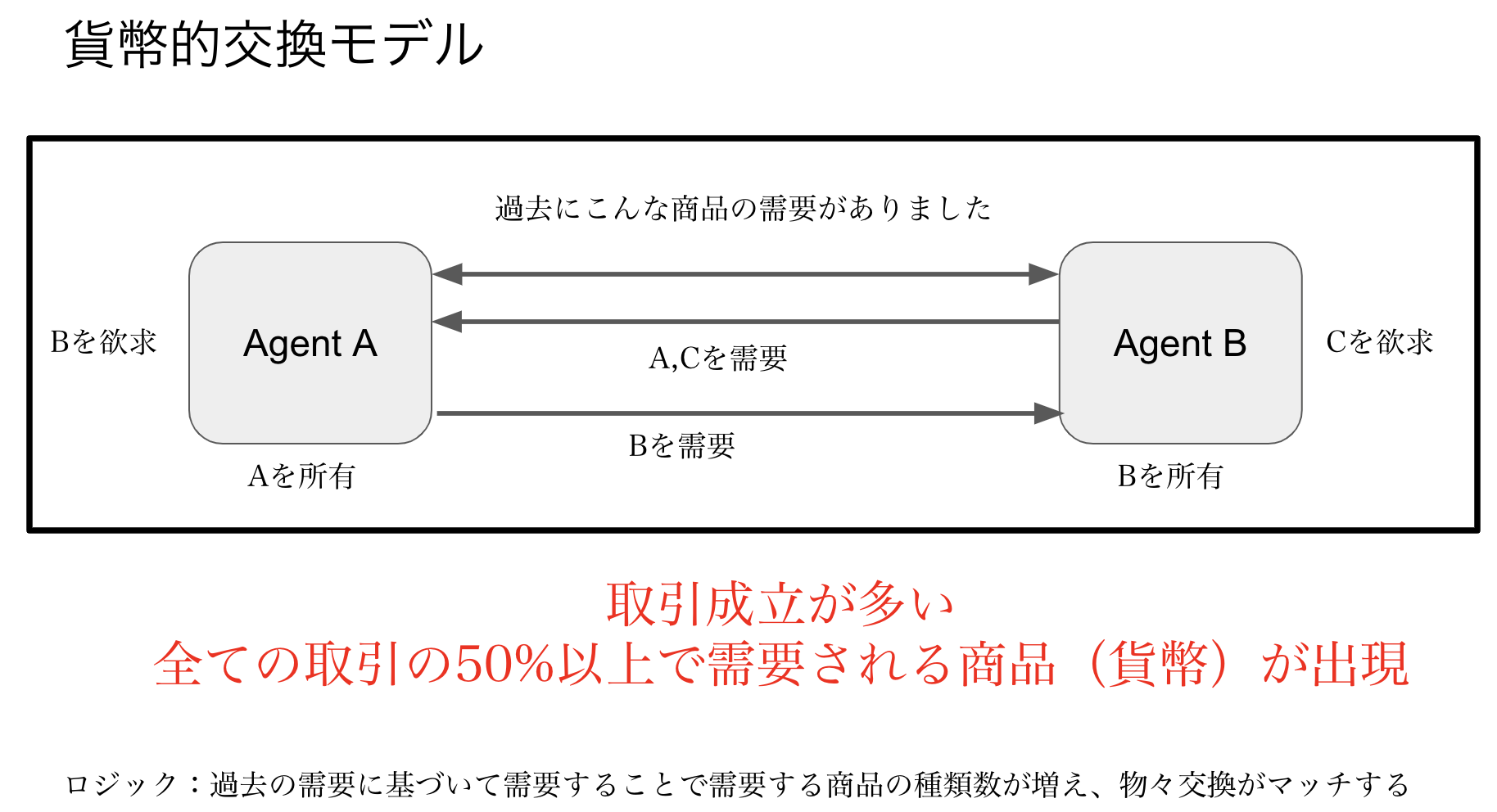
物々交換モデルにおいて、エージェントは自分が欲求する商品だけを需要することで欲望の二重一致の困難が生じ、交換がほとんど行われませんでした。 このモデルでは物々交換モデルに「エージェントはみんなが需要する商品を自分も需要する」というロジックを加えます。
具体的には、以下のような変更を行います。
- エージェントに以下のパラメータを追加する
- $\boldsymbol{v}$ - 視野ベクトル:エージェントが他のエージェントの需要を捉えるためのベクトル
- $m$ - 視野閾値:視野ベクトルの要素がこの値を超えた場合、エージェントはその商品を需要する
- 貨幣出現の定義を$\frac{1}{N} \times \sum_{i=1}^{N}Agent_i.v_j$で0.5を超えるある商品$j$が存在する場合とする
- Step2を書き換える
- 需要算出の前に視野ベクトルを算出する
- 欲求する商品に加え、視野ベクトルのうち視野閾値を超える商品も需要する
- 視野閾値は全てのエージェントで最初に固定する
- 視野ベクトルの初期値は全ての商品について$\frac{1}{N}$とする
パラメータ
書籍では、以下のパラメータが使用されています。
- $N = 50$
- $C = 0.001$
- $P = 0.02$
- $m = 0.078$
エージェントの行動ステップ
Step2以外は物々交換モデルと同じです。
Step2'
需要ベクトルの算出で自分の欲求$w$のみならず、視野ベクトルのうち視野閾値を超えた商品も需要ベクトルに加えます。
Step2’-1: 視野ベクトルの算出
エージェントAとBの視野ベクトルを以下のように算出します。 全ての商品$j$について、 $Agent_A.d_j \gt 0$なら $$Agent_A.v_j \mathrel{+}= \frac{1}{N}$$とします。 これはエージェントBも同様です。
その後、$x_j = \frac{Agent_A.v_j + Agent_B.v_j}{2}$として、$Agent_A.v_j = x_j$、$Agent_B.v_j = x_j$とします。 また、視野ベクトルは以下を満たすように規格化します。 $$\sum_{j=1}^{N}Agent_A.v_j = 1$$ これはエージェントBも同様です。
Step2’-2: 需要ベクトルの算出
[1] $j = Agent_A.w$の時
物々交換モデルのStep2と同様に
エージェントAの欲求する商品$w_a$($w_a = Agent_{A}.w$)について $Agent_A.d_{w_a} = Agent_B.h_{w_a}$
[2] $j \ne Agent_A.w$の時
視野ベクトルを考慮します。 つまり、$Agent_B.h_j \gt 0$かつ$Agent_A.v_j \gt Agent_A.m$の場合、$Agent_A.d_j = Agent_B.h_j$とします。
これ([1]と[2])は、エージェントBも同様です。
結果
視野閾値によって結果が4パターン存在することが確認されます。 この4パターンはそれぞれ以下のように分類されています。
| 戦略 | 視野閾値 | 貨幣が最初から存在しない場合 | 貨幣が最初から存在する場合 |
|---|---|---|---|
| 物々交換戦略 | 0.45~1.0 | 生成しない | 崩壊する |
| 貨幣使用戦略 | 0.12~0.45 | 生成しない | 崩壊しない |
| 貨幣生成戦略 | 0.04~0.12 | 生成する | 崩壊しない |
| 無制限受取戦略 | 0~0.04 | - | - |
無制限受取戦略は、何でもかんでも受け取るため、貨幣は存在しませんが交換は活発です。 視野閾値はパラメータによって変わります。
進化的モデル
貨幣的交換モデルでは視野閾値が全てのエージェントで初期固定ですが、進化的モデルではエージェントの視野閾値を進化的に変更します。
- 視野閾値の初期値は全てのエージェントでランダムに設定する
- 下位$R$エージェントの視野閾値を上位$R$エージェントの視野閾値に変更する
- 閾値入れ替えの設定だけでは閾値の多様性が減少し最終的には収束するため、$T$ターン毎に全エージェントの視野閾値に平均0で分散$\mu$の正規分布に従う乱数を加える
パラメータ
書籍では、以下のパラメータが使用されています。
- $N = 50$
- $C = 0.0001$
- $P = 0.02$
- $R = 3$
- $T = 1024$
- $\mu = 0.00005$
エージェントの行動ステップ
行動ステップは貨幣的交換モデルと同じですが、Step4の後に上記の
- 下位$R$エージェントの視野閾値を上位$R$エージェントの視野閾値に変更する
- 閾値入れ替えの設定だけでは閾値の多様性が減少し最終的には収束するため、$T$ターン毎に全エージェントの視野閾値に平均0で分散$\mu$の正規分布に従う乱数を加える
を実行します。
結果
物々交換→生成→崩壊→物々交換→生成→崩壊というサイクルが確認されます。 また、視野閾値の変化が重要な役割を果たしていることが確認されます。
貨幣が存在しない最初の段階では、貨幣生成戦略が最も有利な戦略となります。
貨幣が生成すると、貨幣使用戦略が最も有利な戦略となります。
閾値が下がり、貨幣使用戦略の上限に近い閾値のエージェントが数人いると貨幣が崩壊します。
閾値の変化は戦略の変化を意味し、このモデルでは戦略の変化によるエージェント間の競争を導入したと言えるでしょう。